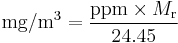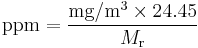Parts-per notation

Parts-per notation is used, especially in science and engineering, to denote relative proportions in measured quantities; particularly in low-value (high-ratio) proportions at the parts-per-million (ppm) 10–6, parts-per-billion (ppb) 10–9, and parts-per-trillion (ppt) 10–12 level. Since parts-per notations are quantity-per-quantity measures, they are known as dimensionless quantities; that is, they are pure numbers with no associated units of measurement. In regular prose, parts-per notations generally take the literal “parts per” meaning of a comparative ratio. However, in mathematical expressions, parts-per notations function as coefficients with values less than 1.
Contents |
Overview
Parts-per notation is often used in the measure of dilutions (concentrations) in chemistry; for instance, for measuring the relative abundance of dissolved minerals or pollutants in water. The expression “1 ppm” means a given property exists at a relative proportion of one part per million parts examined, as would occur if a water-borne pollutant was present at a concentration of one-millionth of a gram per gram of sample solution.
Similarly, parts-per notation is used also in physics and engineering to express the value of various proportional phenomena. For instance, a special metal alloy might expand 1.2 micrometers per meter of length for every degree Celsius and this would be expressed as “α = 1.2 ppm/°C.” Parts-per notation is also employed to denote the change, stability, or uncertainty in measurements. For instance, the accuracy of land-survey distance measurements when using a laser rangefinder might be 1 millimeter per kilometer of distance; this could be expressed as “Accuracy = 1 ppm.”[1]
Parts-per notations are all dimensionless quantities: in mathematical expressions, the units of measurement always cancel. In fractions like “2 nanometers per meter” (2 nm/m = 2 nano = 2 × 10–9 = 2 ppb = 2 × 0.000000001) so the quotients are pure-number coefficients with positive values less than 1. When parts-per notations, including the percent symbol (%), are used in regular prose (as opposed to mathematical expressions), they are still pure-number dimensionless quantities. However, they generally take the literal “parts per” meaning of a comparative ratio (e.g., “2 ppb” would generally be interpreted as “two parts in a billion parts”).[2]
Although the International Bureau of Weights and Measures (an international standards organization known also by its French-language initials BIPM) recognizes the use of parts-per notation, it is not formally part of the International System of Units (SI).[2] Consequently, according to IUPAP, “a continued source of annoyance to unit purists has been the continued use of percent, ppm, ppb, and ppt.”[3] Also, because the named numbers starting with a “billion” have different values in different countries, the BIPM suggests avoiding the use of “ppb” and “ppt” to prevent misunderstanding. Nevertheless, parts-per notation, particularly the expression “ppm”, remains widely used in technical disciplines because of its convenience in denoting dimensionless quantities. See Alternatives to parts-per notation, below.
Parts-per expressions
- One part per hundred is generally represented by the percent (%) symbol and denotes one part per 100 parts, one part in 102, and a value of 1 × 10–2. This is equivalent to one drop of water diluted into 5 milliliters (one spoon-full), or about fifteen minutes out of one day.
- One part per thousand is generally spelled out in full and not as “ppt” (which is usually understood to represent “parts per trillion”). It may also be denoted by the permille (‰) symbol. Note however, that specific disciplines such as the analysis of ocean water salt concentration and educational exercises occasionally use the “ppt” abbreviation. “One part per thousand” denotes one part per 1000 parts, one part in 103, and a value of 1 × 10–3. This is equivalent to one drop of water diluted into 50 milliliters (ten spoon-fulls), or about one and a half minutes out of one day.
- One part per ten thousand is denoted by the permyriad (‱) symbol. It is used almost exclusively in finance, where it is known as the basis point and is typically used to denote fractional changes in percentages. For instance, a change in an interest rate from 5.15% to 5.35% would be denoted as a change of 20 basis points or 20 ‱. Although rarely used in science (ppm is typically used instead), one permyriad has an unambiguous value of one part per 10,000 parts, one part in 104, and a value of 1 × 10–4. This is equivalent to one drop of water diluted into half a liter, or about nine seconds out of one day.
- One part per million (ppm) denotes one part per 1,000,000 parts, one part in 106, and a value of 1 × 10–6. This is equivalent to one drop of water diluted into 50 liters (roughly the fuel tank capacity of a compact car), or about thirty seconds out of a year.
- One part per billion (ppb) denotes one part per 1,000,000,000 parts, one part in 109, and a value of 1 × 10–9. This is equivalent to one drop of water diluted into 250 chemical drums (50 m3), or about three seconds out of a century.
- One part per trillion (ppt) denotes one part per 1,000,000,000,000 parts, one part in 1012, and a value of 1 × 10–12. This is equivalent to one drop of water diluted into 20 Olympic-size swimming pools (50,000 m3), or about three seconds out of every hundred thousand years.
- One part per quadrillion (ppq) denotes one part per 1,000,000,000,000,000 parts, one part in 1015, and a value of 1 × 10–15. This is equivalent to 1 drop of water diluted into a cube of water measuring approximately 368 meters on a side (fifty million cubic meters, which is a cube about as tall as the roof of the Empire State Building), or two and a half minutes out of the age of the Earth (4.5 billion years). Although relatively uncommon in analytic chemistry, measurements at the ppq level are performed.[4]
Alternatives to parts-per notation
SI-compliant expressions
In the English language, named numbers have a consistent meaning only up to “million”. Starting with “billion”, there are two numbering conventions: the “long” and “short” scales, and “billion” can mean either 109 or 1012.
For most of the 19th and 20th centuries, the United Kingdom uniformly used the long scale, while the United States of America used the short scale, so that the two systems were often referred to as “British” and “American” usage respectively. Today, the UK uses the short scale exclusively in official and mass media usage and, although some long-scale usage still continues, the terms “British” and “American” no longer reflect usage (see also Long and short scales). However, the long scale is dominant in many non-English-speaking areas, including continental Europe and Spanish-speaking countries in Latin America (see also Names of large numbers).
Although the BIPM recognizes the use of “parts per million” (ppm) to represent dimensionless quantities, it cautions that due to the above-mentioned language differences and also because “ppt” occasionally means “parts per thousand,” both “ppb” and “ppt” should be avoided to prevent misunderstanding.[2] Clearly, this admonition would also apply to “parts per quadrillion” (ppq) for the same language-based reason. The U.S. National Institute of Standards and Technology (NIST) takes a more stringent position, stating that “the language-dependent terms ‘part per million,’ ‘part per billion,’ and ‘part per trillion’…are not acceptable for use with the SI to express the values of quantities.”[5] Note however, that the NIST’s stated premise for its position is only partially true; “million” has only one meaning in all languages. Note too, that although “percent” (%) is not formally part of the SI, both the BIPM and the ISO, take the position that “in mathematical expressions, the internationally recognized symbol % (percent) may be used with the SI to represent the number 0.01” for dimensionless quantities.[2][6]
Because parts-per notation generally has a well-understood meaning in modern, English-speaking scientific circles, and because its use simplifies the expression of dimensionless quantities, parts-per notation remains widely used in technical disciplines today. Expressions that the BIPM does not explicitly recognize as being suitable for denoting dimensionless quantities with the SI are shown in underlined green text text in the chart below.
| NOTATIONS FOR DIMENSIONLESS QUANTITIES | ||||
|---|---|---|---|---|
| Measure | SI units |
Named parts-per ratio |
Parts-per abbreviation or symbol |
Value in scientific notation |
| A strain of… | 2 cm/m | 2 parts per hundred | 2% [7] | 2 × 10–2 |
| A sensitivity of… | 2 mV/V | 2 parts per thousand | 2 ‰ | 2 × 10–3 |
| A sensitivity of… | 0.2 mV/V | 2 parts per ten thousand | 2 ‱ | 2 × 10–4 |
| A sensitivity of… | 2 µV/V | 2 parts per million | 2 ppm | 2 × 10–6 |
| A sensitivity of… | 2 nV/V | 2 parts per billion | 2 ppb | 2 × 10–9 |
| A sensitivity of… | 2 pV/V | 2 parts per trillion | 2 ppt | 2 × 10–12 |
| A mass concentration of… | 2 mg/kg | 2 parts per million | 2 ppm | 2 × 10–6 |
| A mass concentration of… | 2 µg/kg | 2 parts per billion | 2 ppb | 2 × 10–9 |
| A mass concentration of… | 2 ng/kg | 2 parts per trillion | 2 ppt | 2 × 10–12 |
| A mass concentration of… | 2 pg/kg | 2 parts per quadrillion | 2 ppq | 2 × 10–15 |
| A volume concentration of… | 5.2 µL/L | 5.2 parts per million | 5.2 ppm | 5.2 × 10–6 |
| A molar concentration of… | 5.24 µmol/mol | 5.24 parts per million | 5.24 ppm | 5.24 × 10–6 |
| A stability of… | 1 (µA/A)/min. | 1 part per million per min. | 1 ppm/min. | 1 × 10–6/min. |
| A change of… | 5 nΩ/Ω | 5 parts per billion | 5 ppb | 5 × 10–9 |
| An uncertainty of… | 9 µg/kg | 9 parts per billion | 9 ppb | 9 × 10–9 |
| A shift of… | 1 nm/m | 1 part per billion | 1 ppb | 1 × 10–9 |
| A strain of… | 1 µm/m | 1 part per million | 1 ppm | 1 × 10–6 |
| A temperature coefficient of… | 0.3 (µHz/Hz)/°C | 0.3 part per million per °C | 0.3 ppm/°C | 0.3 × 10–6/°C |
| A frequency change of… | 0.35 × 10–9 ƒ | 0.35 part per billion | 0.35 ppb | 0.35 × 10–9 |
Note that the notations in the “SI units” column above are all dimensionless quantities; that is, the units of measurement cancel in expressions like “1 nm/m” (1 nm/m = 1 nano = 1 × 10–9) so the quotients are pure-number coefficients with values less than 1.
Uno
Because of the cumbersome nature of expressing certain dimensionless quantities per SI guidelines, the International Union of Pure and Applied Physics (IUPAP) in 1999 proposed the adoption of the special name “uno” (symbol: U) to represent the number 1 in dimensionless quantities.[3] This symbol is not to be confused with the always-italicized symbol for the variable ‘uncertainty’ (symbol: U). This unit name uno and its symbol could be used in combination with the SI prefixes to express the values of dimensionless quantities which are much less—or even greater—than one.[8]
Common parts-per notations in terms of the uno are given in the table below.
| Coefficient | Parts-per example | Uno equiv. | Symbol form | Value of quantity |
|---|---|---|---|---|
| 10–2 | 2% | 2 centiuno | 2 cU | 2 × 10–2 |
| 10–3 | 2 ‰ | 2 milliuno | 2 mU | 2 × 10–3 |
| 10–6 | 2 ppm | 2 microuno | 2 µU | 2 × 10–6 |
| 10–9 | 2 ppb | 2 nanouno | 2 nU | 2 × 10–9 |
| 10–12 | 2 ppt | 2 picouno | 2 pU | 2 × 10–12 |
In 2004, a report to the International Committee for Weights and Measures (known also by its French-language initials CIPM) stated that response to the proposal of the uno “had been almost entirely negative” and the principal proponent “recommended dropping the idea.”[9] To date, the uno has not been adopted by any standards organization and it appears unlikely it will ever become an officially sanctioned way to express low-value (high-ratio) dimensionless quantities. The proposal was instructive, however, as to the perceived shortcomings of the current options for denoting dimensionless quantities.
Improper applications of parts-per notation
Parts-per notation may properly be used only to express true dimensionless quantities; that is, the units of measurement must cancel in expressions like “1 mg/kg” so that the quotients are pure numbers with values less than 1. Mixed-unit quantities such as “a radon concentration of 15 pCi/L” are not dimensionless quantities and may not be expressed using any form of parts-per notation, such as “15 ppt”. Other examples of measures that are not dimensionless quantities are as follows:
- Particulate matter in the air: 50 µg/m3 but not: 50 ppb. Also see Air measurements, below.
- A stepper motor/gear system that produces a motion of 1 µm/pulse but not: 1 ppm
- Mercury vapor concentration in air: 0.6 ng/L but not: 0.6 ppt
Note however, that it is not uncommon to express aqueous concentrations—particularly in drinking-water reports intended for the general public—using parts-per notation (2.1 ppm, 0.8 ppb, etc.) and further, for those reports to state that the notations denote milligrams per liter or micrograms per liter. Whereas “2.1 mg/L” is technically not a dimensionless quantity on the face of it, it is well understood in scientific circles that one liter of water has a mass of one kilogram and that “2.1 mg/kg” (2.1 ppm) is the true measure. The goal in all technical writing (including drinking-water reports for the general public) is to clearly communicate to the intended audience with minimal confusion. Drinking water is intuitively a volumetric quantity in the public’s mind so measures of contamination expressed on a per-liter basis are considered to be easier to grasp. Still, it is technically possible, for example, to "dissolve" more than one liter of a very hydrophilic chemical in 1 liter of water; parts-per notation would be confusing when describing its solubility in water (greater than a million parts per million), so one would simply state the volume (or mass) that will dissolve into a liter, instead.
When reporting air-borne rather than water-borne densities, a slightly different convention is used since air is approximately 1000 times less dense than water. In water, 1 µg/m3 is roughly equivalent to parts-per-trillion whereas in air, it is roughly equivalent to parts-per-billion. Note also, that in the case of air, this convention is much less accurate. Whereas one liter of water is almost exactly 1 kg; one cubic meter of air is often taken as 1.143 kg—close enough for many practical uses.
Convertibility to other units of measurement
Parts-per notations may be expressed in terms of any unit of the same measure. For instance, the coefficient of thermal expansion of a certain brass alloy, α = 18.7 ppm/°C, may be expressed as 18.7 (µm/m)/°C, or as 18.7 (µin/in)/°C; the numeric value representing a relative proportion does not change with the adoption of a different unit of measure.[10] Similarly, a metering pump that injects a trace chemical into the main process line at the proportional flow rate Qp = 125 ppm, is doing so at a rate that may be expressed in a variety of volumetric units, including 125 µL/L, 125 µgal/gal, 125 µ(m3)/m3, etc.
Air measurements
Often, parts-per notation is the simplest and best measure. But other times, it is less suitable or even impossible. This sometimes results in agencies such as the World Health Organization or US EPA presenting entire tables of air concentrations that use the weight/volume method, when parts-per notation might have more readily worked for many (but not all) substances present. While many contaminants can be easily described using parts-per notation, a few of them present a much more complex picture.
A case in point is when measuring gasoline (a.k.a. petrol). It's a very complex mixture which might have dozens or hundreds of types of molecules present, in air. It would require sophisticated, extremely expensive analysis to enumerate all of a given sample's molecules and give it an accurate parts-per measurement - and that measurement would probably not be comparable to any other gasoline parts-per concentration, because the petroleum mixture of the second sample would be different. (Batches of petroleum product differ considerably; as an extreme example, gasoline fractions have a far higher parts-per count - many more molecules per molecule of air - compared to a heavier petroleum product like diesel, for a given weight per volume measure at STP.) Therefore, a mass per volume concentration unit (such as mg/m3) is almost always used for petroleum vapors, as well as for certain other complex mixtures.
If one is dealing with a single known diluent (contaminant), it is easy to convert from parts-per notation to mass per volume concentration, using the substance's molecular weight (Mr) in the following types of equations:
For example, 1 ppm of toluene (Mr = 92.15 g/mol) is equivalent to a 3.8 mg/m3 concentration. The constant 24.45 L/mol is the molar volume of an ideal gas at 25 °C and 1 atmosphere: for different pressures and temperatures, this value needs to be recomputed.
See also
|
|
References
- ↑ This is a simplified explanation. Laser rangefinders typically have a measurement granularity of one to ten millimeters; thus, the complete specification for distance measurement accuracy might read as follows: Accuracy: ±(1 mm + 1 ppm). Consequently, a distance measurement of only a few meters would still have an accuracy of ±1 mm in this example.
- ↑ 2.0 2.1 2.2 2.3 BIPM: 5.3.7 Stating values of dimensionless quantities, or quantities of dimension one
- ↑ 3.0 3.1 Report to the 1999 IUPAP General Assembly: Report on recent Committee activities on behalf of IUPAP by Brian W Petley September 1998
- ↑ Measurements of dioxin are routinely made at the sub-ppq level. The U.S. Environmental Protection Agency (EPA) currently sets a hard limit of 30 ppq for dioxin in drinking water but once recommended a voluntary limit of 0.013 ppq. Also, radioactive contaminants in drinking water, which are quantified by measuring their radiation, are often reported in terms of ppq. The ability to chemically detect contaminants at this level is truly an impressive feat; 0.013 ppq is equivalent to the thickness of a sheet of paper versus a journey of 146,000 trips around the world.
- ↑ NIST: Rules and Style Conventions for Expressing Values of Quantities: 7.10.3 ppm, ppb, and ppt
- ↑ Quantities and units - Part 0: General principles, ISO 31-0:1992.
- ↑ Compliance with the SI regarding the percent symbol (%) is limited in this chart. According to the BIPM’s SI brochure: Subsection 5.3.3, Formatting the value of a quantity, a space is always used to separate the unit symbol from the numeric value. Notable exceptions are the unit symbols for degree, minute, and second for plane angle, °, ′, and ″ (e.g., a latitude of 47° 38′ 8.8″). However, according to 5.3.7 Stating values of dimensionless quantities, or quantities of dimension one, the exception does not apply to the “%” symbol; it states as follows: “When it [the percent symbol] is used, a space separates the number and the symbol %.” This practice has not been well adopted with regard to the % symbol, is contrary to Wikipedia’s Manual of Style, and is not observed here.
- ↑ Certain mathematical functions can produce proportional quantities with values greater than 1.
- ↑ Report of the 16th meeting (13–14 May 2004), by the Consultative Committee for Units, to the International Committee for Weights and Measures, of the International Bureau of Weights and Measures (1.1 MB PDF, here).
- ↑ In the particular case of coefficient of thermal expansion, the change to inches (one of the U.S. customary units) is typically also accompanied by a change to degrees Fahrenheit. Since a Fahrenheit-sized interval of temperature is only 5⁄9 that of a Celsius-sized interval, the value is typically expressed as 10.4 (µin/in)/°F rather than 18.7 (µin/in)/°C.
External links
- National Institute of Standards and Technology (NIST): Home page
- International Bureau of Weights and Measures (BIPM): Home page
- Concentration Calculator and Concentration Converter